高考资讯 所处位置:首页 > 高考资讯
高一数学人教新目标版期末试题 北京大学生家教网
来源:北师大家教网
高一数学人教新目标版期末试题
北京大学生家教网
一、选择题
1. 已知集合M={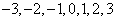 },集合N={
},集合N={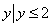 },则M
},则M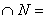
A. {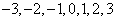 } B. {
} B. { }
}
C. {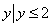 } D.
} D. 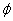
2. 若函数y=f(x)的定义域是[1,2],则y=f(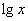 )的定义域是
)的定义域是
A. [1,2] B. [2,4] C. [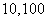 ] D. [
] D. [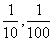 ]
]
3. 已知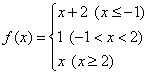 ,若
,若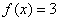 ,则
,则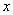 的值是
的值是
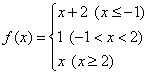 ,若
,若A. 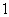 B.
B. 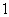 或3 C.
或3 C.  或
或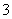 D. 3
D. 3
4. 下列函数与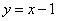 有相同图象的是
有相同图象的是
A. 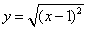 B.
B. 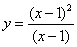
C. 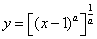
 D.
D. 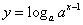
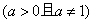
5. 设偶函数f(x)的定义域为R,当x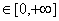 时f(x)是增函数,则f(2),f(
时f(x)是增函数,则f(2),f(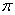 ),f(-3)的大小关系是
),f(-3)的大小关系是
A. f(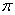 )>f(-3)>f(2) B. f(
)>f(-3)>f(2) B. f(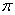 )>f(2)>f(-3)
)>f(2)>f(-3)
C. f(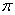 )<f(-3)<f(2) D. f(
)<f(-3)<f(2) D. f(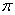 )<f(2)<f(-3)
)<f(2)<f(-3)
6. 已知向量a=( ,1),b是不平行于x轴的单位向量,且a·b=
,1),b是不平行于x轴的单位向量,且a·b= ,则b等于( )
,则b等于( )
A.( ,
,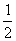 ) B.(
) B.(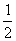 ,
, ) C.(
) C.(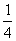 ,
,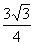 ) D.(1,0)
) D.(1,0)
7. 已知|a|=1,|b|=2,a与b的夹角为60°,c=2a+3b,d=ka-b(k∈R),且c⊥d,那么k的值为( )
A. -6 B. 6 C. 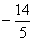 D.
D. 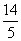
8. 将函数y=sinωx(ω>0)的图象按向量a=(- ,0)平移,平移后的图象如图所示,则平移后的图象所对应函数的解析式是( )
,0)平移,平移后的图象如图所示,则平移后的图象所对应函数的解析式是( )
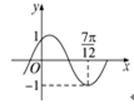
A. y=sin(x+ ) B. y=sin(x-
) B. y=sin(x- )
)
C. y=sin(2x+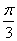 ) D. y=sin(2x-
) D. y=sin(2x-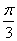 )
)
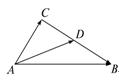
9. 已知|p|=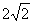 ,|q|=3,p、q的夹角为
,|q|=3,p、q的夹角为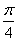 ,如图所示,若
,如图所示,若 =5p+2q,
=5p+2q,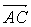 =p-3q,D为BC的中点,则|
=p-3q,D为BC的中点,则|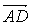 |为( )
|为( )
A. 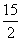 B.
B. 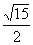 C. 7 D. 18
C. 7 D. 18
10. 要得到函数y=sin(2x-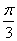 )的图象,只要将函数y=sin2x的图象( )
)的图象,只要将函数y=sin2x的图象( )
A. 向左平行移动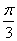 个单位 B. 向左平行移动
个单位 B. 向左平行移动 个单位
个单位
C. 向右平行移动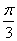 个单位 D. 向右平行移动
个单位 D. 向右平行移动 个单位
个单位
11. 如果|cosθ|=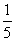 ,
,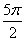 <θ<3π,那么sin
<θ<3π,那么sin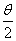 的值等于( )
的值等于( )
A. 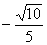 B.
B. 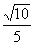 C.
C. 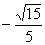 D.
D. 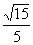
12. 函数y=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+f(3)+…+f(11)的值等于( )
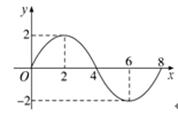
A. 2 B. 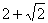 C.
C. 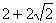 D.
D. 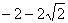
二、填空题
13. 已知函数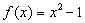 ,则函数
,则函数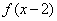 的零点是__________。
的零点是__________。
14. 若函数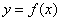 的图象关于直线
的图象关于直线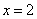 对称,并且方程
对称,并且方程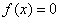 有三个实根,则这三个实根的和为 。
有三个实根,则这三个实根的和为 。
15. 已知 =2e1+ke2,
=2e1+ke2,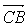 =e1+3e2,
=e1+3e2,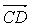 =2e1-e2,若A、B、D三点共线,则k=____________。
=2e1-e2,若A、B、D三点共线,则k=____________。
16. 给出下列四个命题:
①函数y=tanx的图象关于点(kπ+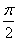 ,0)(k∈Z)对称;
,0)(k∈Z)对称;
②函数f(x)=sin|x|是最小正周期为π的周期函数;
③设θ为第二象限的角,则tan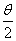 >cos
>cos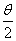 ,且sin
,且sin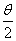 >cos
>cos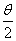 ;
;
④函数y=cos2x+sinx的最小值为-1。
其中正确的命题是________________________________________。
三、解答题
17. 已知cosα= ,且-
,且-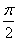 <α<0,求
<α<0,求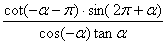 的值。
的值。
18. 已知向量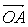 =(3,-4),
=(3,-4),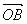 =(6,-3),
=(6,-3),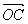 =(5-m,-(3+m))。
=(5-m,-(3+m))。
(1)若点A、B、C能构成三角形,求实数m应满足的条件;
(2)若△ABC为直角三角形,且∠A为直角,求实数m的值。
19. 已知f(x)=sin(2x+ )+sin(2x-
)+sin(2x- )+2cos2x+a,当x∈[-
)+2cos2x+a,当x∈[-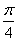 ,
,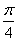 ]时,f(x)的最小值为-3,求a的值。
]时,f(x)的最小值为-3,求a的值。
20. 已知点A、B、C的坐标分别为A(3,0)、B(0,3)、C(cosα,sinα),α∈(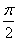 ,
,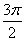 )。
)。
(1)若|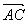 |=|
|=|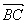 |,求角α的值;
|,求角α的值;
(2)若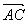 ·
·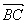 =-1,求
=-1,求 的值。
的值。
21. (本小题满分11分)设关于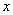 的函数
的函数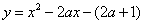
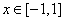 。
。
(Ⅰ)若当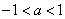 时,判断函数
时,判断函数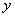 的单调区间;
的单调区间;
(Ⅱ)若函数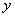 的最小值为
的最小值为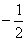 ,试确定满足条件的
,试确定满足条件的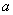 的值;
的值;
(Ⅲ)对(Ⅱ)中的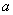 值,求函数
值,求函数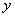 的最大值。
的最大值。
试题答案
一、选择题
1、B 解析:直接利用交集定义即可求出。
2、C 解析:由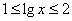 ,解得
,解得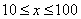 。
。
3、D 解析:当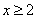 时,由题意得
时,由题意得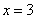 。
。
4、D 解析:通过比较解析式、定义域和值域可得。
5、A 解析:由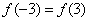 ,当x
,当x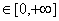 时f(x)是增函数,得f(
时f(x)是增函数,得f(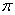 )>f(3)>f(2),即f(
)>f(3)>f(2),即f(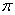 )>f(-3)>f(2)。
)>f(-3)>f(2)。
6、B 解析:b为单位向量,∴设b=(cosθ,sinθ)。
∵a·b= ,∴(
,∴( ,1)·(cosθ,sinθ)=
,1)·(cosθ,sinθ)= cosθ+sinθ=
cosθ+sinθ= 。
。
∴sin(θ+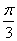 )=sin
)=sin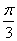 .∴θ+
.∴θ+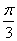 =
=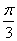 或θ+
或θ+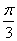 =π-
=π-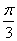 .∴θ=0或θ=
.∴θ=0或θ=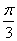 。
。
当θ=0时,b=(1,0),b∥x轴,不合题意舍去。
当θ=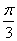 时,b=(
时,b=(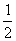 ,
, )。
)。
7、D 解析:a·b=1×2×cos60°=1,∵c⊥d,
∴c·d=(2a+3b)·(ka-b)=2ka2-2a·b+3ka·b-3b2=2k-2+3k-12=0.∴k=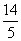 。
。
8、C 解析:将函数y=sinωx(ω>0)的图象按向量a=(- ,0)平移,平移后的图象所对应的解析式为y=sinω(x+
,0)平移,平移后的图象所对应的解析式为y=sinω(x+ )。由图象知,ω(
)。由图象知,ω(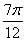 +
+ )=
)=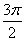 ,所以ω=2,因此选C。
,所以ω=2,因此选C。
9、A 解析: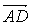 =
=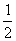 (
(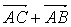 )=
)=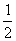 (5p+2q+p-3q)=
(5p+2q+p-3q)=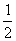 (6p-q),
(6p-q),
∴|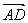 |=
|=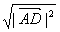 =
=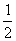
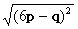
=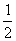
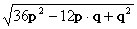 =
=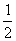
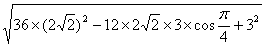 =
=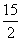 。
。
10、D 解析:由y=sin2x到y=sin(2x-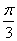 )关键是看x的变化,即由x到x-
)关键是看x的变化,即由x到x- ,所以需向右平行移动
,所以需向右平行移动 个单位。
个单位。
11、C 解析:由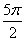 <θ<3π,可知cosθ<0,则|cosθ|=-cosθ=
<θ<3π,可知cosθ<0,则|cosθ|=-cosθ=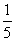 ,cosθ=-
,cosθ=-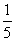 。
。
又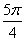 <
<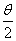 <
<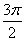 ,则sin
,则sin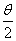 <0.于是sin
<0.于是sin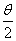 =
=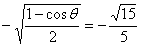 。
。
12、C 解析:由图象可知,f(x)=2sin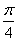 x的周期为8,
x的周期为8,
∴f(1)+f(2)+f(3)+…+f(11)=f(1)+f(2)+f(3)=2sin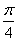 +2sin
+2sin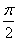 +2sin
+2sin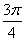 =2+
=2+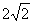 。
。
二、填空题
13、1,3 解析: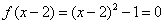 ,解得
,解得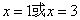 。
。
14、6 解析:由题意必有一个根是2,另外两个根关于x=2对称,所以三者之和为6。
15、-8 解析:若A、B、D三点共线,则 ∥
∥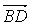 ,设
,设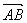 =λ
=λ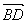 。
。
∵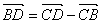 =e1-4e2,
=e1-4e2,
∴2e1+ke2=λ(e1-4e2)=λe1-4λe2。
∴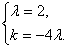 ∴k=-8。
∴k=-8。
16、①④ 解析:①由正切曲线,知点(kπ,0),(kπ+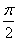 ,0)
,0)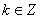 是正切函数的对称中心,∴①对。
是正切函数的对称中心,∴①对。
②f(x)=sin|x|不是周期函数,②错。
③∵θ∈(2kπ+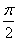 ,2kπ+π),k∈Z,∴
,2kπ+π),k∈Z,∴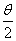 ∈(kπ+
∈(kπ+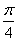 ,kπ+
,kπ+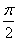 )。
)。
当k=2n+1,k∈Z时,sin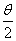 <cos
<cos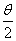 。∴③错。
。∴③错。
④y=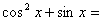 1-sin2x+sinx=-(sinx
1-sin2x+sinx=-(sinx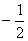 )2+
)2+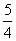 ,∴当sinx=-1时,ymin=1-(-1)2+(-1)=-1。∴④对。
,∴当sinx=-1时,ymin=1-(-1)2+(-1)=-1。∴④对。
三、解答题
17、解:∵cosα= ,且-
,且-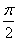 <α<0,∴sinα=-
<α<0,∴sinα=-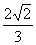 ,cotα=
,cotα=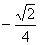 。
。
∴原式=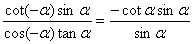 =-cotα=
=-cotα=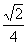 。
。
18、解:(1)已知向量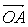 =(3,-4),
=(3,-4),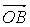 =(6,-3),
=(6,-3),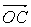 =(5-m,-(3+m)),若点A、B、C能构成三角形,则这三点不共线。
=(5-m,-(3+m)),若点A、B、C能构成三角形,则这三点不共线。
∵ =(3,1),
=(3,1),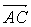 =
=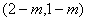
∴3(1-m)≠2-m。
∴当实数m≠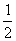 时满足条件。
时满足条件。
(若要使点A、B、C能构成三角形,则必须满足|AB|+|BC|>|CA|)
(2)若△ABC为直角三角形,且∠A为直角,则 ⊥
⊥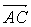 ,
,
∴3(2-m)+(1-m)=0,解得m=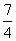 。
。
19、解:∵f(x)=sin(2x+ )+sin(2x-
)+sin(2x- )+2cos2x+a
)+2cos2x+a
= sin2x+cos2x+1+a=2sin(2x+
sin2x+cos2x+1+a=2sin(2x+ )+1+a,
)+1+a,
x∈[-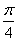 ,
,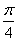 ],∴-
],∴-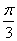 ≤2x+
≤2x+ ≤
≤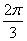 。
。
∴f(x)在[-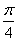 ,
,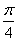 ]上的最小值为2(-
]上的最小值为2(- )+1+a=1-
)+1+a=1- +a。
+a。
由题意知1- +a=-3,∴a=
+a=-3,∴a= -4。
-4。
20、解:(1)∵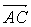 =(cosα-3,sinα),
=(cosα-3,sinα),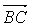 =(cosα,sinα-3),
=(cosα,sinα-3),
∴|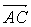 |=
|=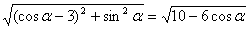 ,
,
|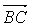 |=
|=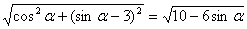 。
。
由|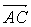 |=|
|=|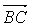 |得sinα=cosα。
|得sinα=cosα。
又∵α∈(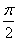 ,
,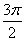 ),∴α=
),∴α=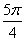 。
。
(2)由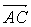 ·
·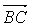 =-1得
=-1得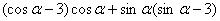 =-1。∴sinα+cosα=
=-1。∴sinα+cosα=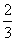 。 ①
。 ①
又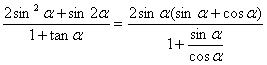 =2sinαcosα。
=2sinαcosα。
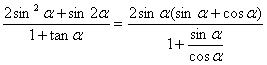 =2sinαcosα。
=2sinαcosα。由①式两边平方得1+2sinαcosα=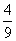 ,
,
∴2sinαcosα=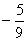 。
。
∴ 。
。
21、解:(Ⅰ)因为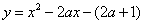
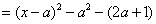 ,对称轴
,对称轴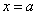 ,
,
又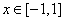 ,
,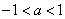 ,则
,则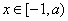 单调递减,
单调递减,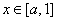 单调递增。
单调递增。
(Ⅱ)当 时,
时,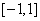 是函数
是函数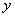 的递增区间,
的递增区间,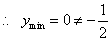 ;
;
当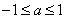 时,
时,
得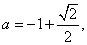 或
或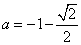 (舍),
(舍),
当 时,
时,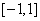 是函数
是函数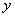 的递减区间,
的递减区间,
综上,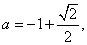
(Ⅲ)此时
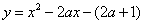
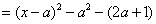 ,
,
当![]() 时
时![]() 。
。
北京家教中心、北京家教网、北京大学生家教网,北京一对一家教,北京家教中介
北师大家教网官方网站:http://www.beishidajiajiao.com/
相关话题:北京家教、北京家教中介、北京家教网、北京大学生家教、北京家教中心
