本试卷分第Ⅰ卷和第Ⅱ卷两部分，满分为110分，考试时间为120分钟。

第Ⅰ卷

一、选择题（每小题4分，共32分。）

1. 下列求导数运算正确的是（ ）

A. B.

C. D.

2. 设曲线在点处的切线与直线垂直，则（ ）

A. 2 B. C. D.

3. 极坐标方程化为直角坐标方程是（ ）

A. B.

C. D.

4. 已知函数，其导函数的图像大致为（ ）

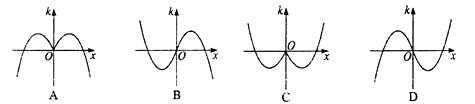
5. 定积分的值为（ ）

A. B. C. D.

6. 设，则集合中元素的个数为（ ）

A. 1 B. 2 C. 3 D. 无数个

7. 要做一个圆锥形漏斗，母线长为20cm，要使其体积最大，则其高应为（ ）

A. B. C. D.

8. 从如图所示的正方形区域内任取一个点，则点取自阴影部分的概率为（ ）

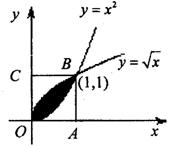
A. B. C. D.

二、填空题（每小题4分，共24分）

9. 复数，，则等于_________________。

10. 函数的单调增区间为_____________，单调减区间为_____________。

11. 极坐标系中，直线的方程是，则点到直线的距离为________。

12. 记等差数列的前项和，利用倒序求和的方法得：；类似的，记等比数列的前项的积为，且，试类比等差数列求和的方法，可将表示成首项，末项与项数的一个关系式，即公式_______________。

13. 如图，在圆内接四边形中，对角线，相交于点。已知，，，则_____________，的长是______________。

14. 已知数列2010，2011，1，－2010，－2011，…，这个数列的特点是从第二项起，每一项都等于它的前后两项之和，则这个数列的前2011项之和等于____________。

第Ⅱ卷

三、解答题（共5个小题，共44分）

15. 已知，求证：

16. 求证：

17. 已知函数，其中实数。

（1）若，求曲线在点处的切线方程；

（2）若在处取得极值，试讨论的单调性。

18. 图中竖直线段和斜线段都表示通道，并且在交点处相遇，若竖直线段有一条的为第一层，有两条的为第二层，以此类推，竖直线段有条的为第层，每一层的竖直通道从左到右分别称为第1通道、第2通道，……，现在有一个小球从入口向下（只能向下，不能向上）运动，小球在每个交点处向左到达下一层或者向右到达下一层的可能性是相同的。小球到达第层第通道的不同路径数称为，如小球到达第二层第1通道和第二层第2通道的路径都只有一种情况，因此，，。

求：（1），，；

（2），以及小球到达第5层第2通道的概率；

（3）猜想，并证明；

（4）猜想（不用证明）。

19. 已知函数

（1）求函数的单调区间和最大值；

（2）若恒成立，求的取值范围；

（3）证明：①在上恒成立；

②

四、附加题（10分）

设是正实数，且。

证明：

【试题答案】

一、选择题

1. B 2. D 3. A 4. B 5. C 6. C 7. A 8. B

二、填空题

9： 10： 11： 12：

13：，6 14：2010

三、解答题

15. 略

16. 略

17. （1）

（2）增区间：和 减区间：

18. （1）1，2，1（2）4，1/4（3）（4）

19. （1）递增，增，减，最大值

（2）

（3）略