高考资讯 所处位置:首页 > 高考资讯
高中数学20分钟专题突破14 北京一对一家教
来源:北师大家教网
高中数学20分钟专题突破14
北京一对一家教
北京一对一家教资料:高中数学20分钟专题突破14
空间向量与立体几何
一.选择题
1.下列命题中,假命题是( )
(A)a、b是异面直线,则一定存在平面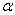 过a且与b平行
过a且与b平行
(B)若a、b是异面直线,则一定存在平面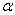 过a且与b垂直
过a且与b垂直
(C)若a、b是异面直线,则一定存在平面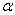 与a、b所成角相等
与a、b所成角相等
(D)若a、b是异面直线,则一定存在平面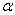 与a、b的距离相等
与a、b的距离相等
2.下列命题中,真命题是( )
(A) 若直线m、n都平行于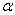 ,则
,则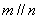
(B) 设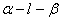 是直二面角,若直线
是直二面角,若直线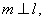 则
则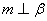
(C) 若m、n在平面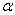 内的射影依次是一个点和一条直线,且
内的射影依次是一个点和一条直线,且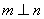 ,则
,则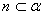 或
或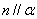
(D) 若直线m、n是异面直线,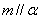 ,则n与
,则n与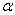 相交
相交
3.如果直线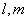 与平面
与平面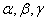 满足:
满足: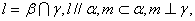 那么必有( )
那么必有( )
(A)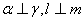 (B)
(B)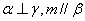
(C)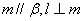 (D)
(D)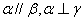
4.设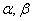 是两个不重合的平面,m和
是两个不重合的平面,m和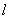 是两条不重合的直线,则
是两条不重合的直线,则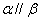 的一个充分条件是( )
的一个充分条件是( )
(A) 且
且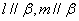 (B)
(B)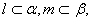 且
且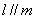
(C)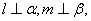 且
且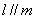 (D)
(D)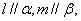 且
且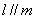
5.已知直二面角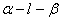 ,直线
,直线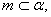 直线
直线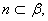 且m、n均不与
且m、n均不与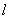 垂直,则( )
垂直,则( )
(A)m、n可能不垂直,但可能平行 (B)m、n可能垂直,但不可能平行
(C)m、n可能垂直,也可能平行 (D)m、n不可能垂直,也不可能平行
6.二面角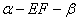 是直二面角,
是直二面角,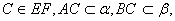 如果∠ACF=30
如果∠ACF=30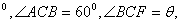 那么
那么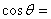 ( )
( )
(A)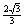 (B)
(B)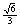
(C)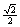 (D)
(D)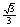
二.填空题
1.13.已知正四棱锥P—ABCD的高为4,侧棱长与底面所成的角为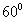 ,则该正四棱锥的侧面积是 .
,则该正四棱锥的侧面积是 .
2.已知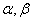 、
、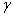 是三个互不重合的平面,
是三个互不重合的平面,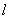 是一条直线,给出下列四个命题:
是一条直线,给出下列四个命题:
①若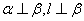 ,则
,则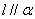 ; ②若
; ②若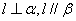 ,则
,则 ;
;
③若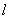 上有两个点到
上有两个点到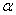 的距离相等,则
的距离相等,则 ; ④若
; ④若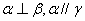 ,则
,则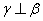 。
。
其中正确命题的序号是
3.正三棱锥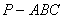 高为2,侧棱与底面成
高为2,侧棱与底面成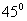 角,则点A到侧面
角,则点A到侧面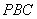 的距离是
的距离是
三.解答题
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,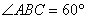 ,E,F分别是BC, PC的中点.
,E,F分别是BC, PC的中点.
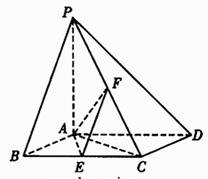
(Ⅰ)证明:AE⊥PD;
(Ⅱ)若H为PD上的动点,EH与平面PAD所成最大角的正切值为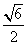 ,求二面角E—AF—C的余弦值.
,求二面角E—AF—C的余弦值.
答案:
一.选择题
1.选B 2.选C 3.选A 4选C 5.选A 6.选D
二.填空题
1. 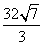 2. ②④ 3.
2. ②④ 3. 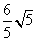
三.解答题
(Ⅰ)证明:由四边形ABCD为菱形,∠ABC=60°,可得△ABC为正三角形.
因为 E为BC的中点,所以AE⊥BC.
又 BC∥AD,因此AE⊥AD.
因为PA⊥平面ABCD,AE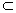 平面ABCD,所以PA⊥AE.
平面ABCD,所以PA⊥AE.
而 PA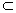 平面PAD,AD
平面PAD,AD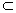 平面PAD 且PA∩AD=A,
平面PAD 且PA∩AD=A,
所以 AE⊥平面PAD,又PD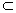 平面PAD.
平面PAD.

所以 AE⊥PD.
(Ⅱ)解:设AB=2,H为PD上任意一点,连接AH,EH.
由(Ⅰ)知 AE⊥平面PAD,
则∠EHA为EH与平面PAD所成的角.
在Rt△EAH中,AE=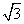 ,
,
所以 当AH最短时,∠EHA最大,
即 当AH⊥PD时,∠EHA最大.
此时 tan∠EHA=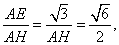
因此 AH=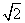 又AD=2,所以∠ADH=45°,.
又AD=2,所以∠ADH=45°,.
所以 PA=2.
解法一:因为 PA⊥平面ABCD,PA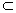 平面PAC,
平面PAC,
所以 平面PAC⊥平面ABCD.
过E作EO⊥AC于O,则EO⊥平面PAC,
过O作OS⊥AF于S,连接ES,则∠ESO为二面角E-AF-C的平面角,
在Rt△AOE中,EO=AE·sin30°=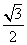 ,AO=AE·cos30°=
,AO=AE·cos30°=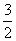 ,
,
又F是PC的中点,在Rt△ASO中,SO=AO·sin45°=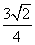 ,
,
又 

在Rt△ESO中,cos∠ESO=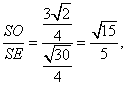
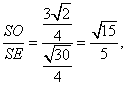
即所求二面角的余弦值为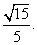
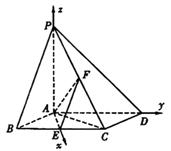
解法二:由(Ⅰ)知AE,AD,AP两两垂直,以A为坐标原点,建立如图所示的空间直角坐标系,又E、F分别为BC、PC的中点,所以E、F分别为BC、PC的中点,所以
A(0,0,0),B(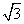 ,-1,0),C(C,1,0),
,-1,0),C(C,1,0),
D(0,2,0),P(0,0,2),E(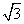 ,0,0),F(
,0,0),F(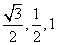 ),
),
所以 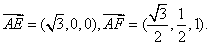
设平面AEF的一法向量为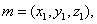
则 因此
因此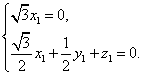
 因此
因此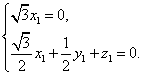
取

因为 BD⊥AC,BD⊥PA,PA∩AC=A,
所以 BD⊥平面AFC,
故 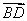 为平面AFC的一法向量.
为平面AFC的一法向量.
又 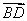 (-
(-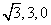 ),=
),=
所以 cos<m, 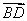 >=
>=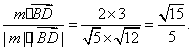
因为 二面角E-AF-C为锐角,
所以所求二面角的余弦值为![]()
![]()
北京家教中心、北京家教网、北京大学生家教网,北京一对一家教,北京家教中介
北师大家教网官方网站:http://www.beishidajiajiao.com/
相关话题:北京家教、北京家教中介、北京家教网、北京大学生家教、北京家教中心
